Barbara Dill (barbaradill.com) began playing with multiple axes / multi-centers turning in the early 1990s. Initially she explored the basics of between centers multi-axes spindle turning, working with pen turning sized square blanks and her tool rest set parallel to the lathe's axis.
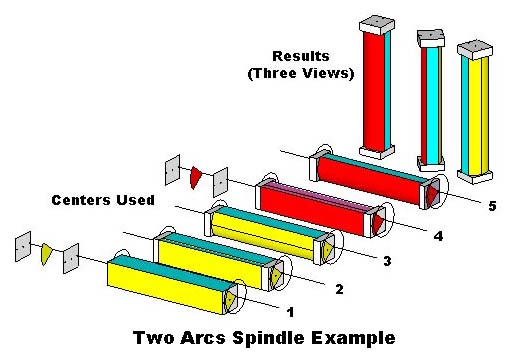
Here's and example of "spindle turning" but on two separate pairs of centers, offset from the center of the blank, and turning an arc rather than full round on each pair of centers. Mount the blank on the Yellow Arc centers and turng the Yellow Arc (1,2 & 3). Then remound the blank on the Red Arc centers and turng the Red Arc (4 & 5). The resulting piece leaves a flat on the blank where the arcs intersect the sides of the blank. Normally the two arcs are turned to intersect each other, leaving no "flat" - but for purposes of illustation . . .
These "virtual 3D examples were done in Google's FREE SketchUp program. You can download a FREE version - for your operating system - install it, then download this and subsequent files to peruse them in virtual 3D. (click here to get SketchUp). And if you need a little help in using SketchUpor want to try the simpler SketchUpViewer - click here.
Frustrated with not being able to predict outcomes, she began developing a structured means of understanding EFFECT and CAUSE - "If I do THIS, then THAT will be what happen.". She's since had several articles on her structured approach to mullti-axes / multi-centers turning published in AAW's Amercian Woodturner magazine. She also has made her paper on the subject available on her website, given demonstrations and talks on the subject and is scheduled as a Demonstrator for the AAW 2012 Symposium to be held in San Jose, California (that's in the San Francisco Bay Area, in the center of Silicon Valley).
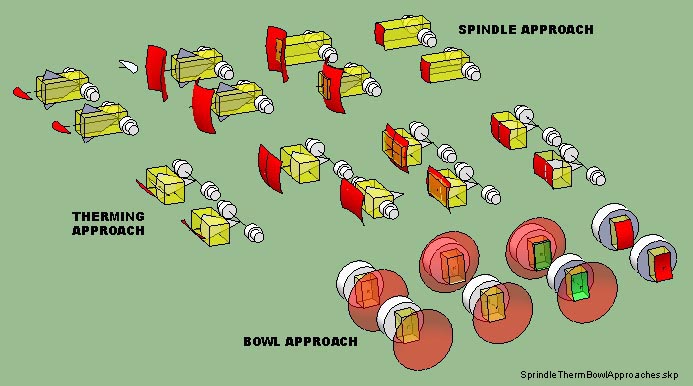
In 2010, wanting to take her multi-axes turning beyond just spindles, Barbara began applying what she'd learned from doing multi-axes spindle turning - to larger pieces - rectangular Tea Pots, Tea Cups and Lidded Bowls with long radii curved surfaces. But a Spindle Turner Approach wouldn't permit turning long radius curves on the SIDES of a tall rectangular blank - the center of the arc's radius would be well outside the blank. Therming WOULD permit long radius curved faces - but it would also involve turning a lot of Air Wood (a term Barbara came up with early in her exploratin of multi-axes turning) - and is a bit more complicated than spindle turning.
And that's where her next breakthrough came - thinking, not in terms of Intersecting ARCS, but rather - thinking in terms of INTERSECTING HEMISPHERES. This shift from thinking as a Sprindle Turner to thinking as a BOWL TURNER opened up a whole new area to explore.
Here's where THAT lead.

(Photo courtesy of Barbara Dill)
Using Google's FREE SketchUp 3D modeling program, I THINK I've worked out the HOW of Barbara's Tea Pot form.
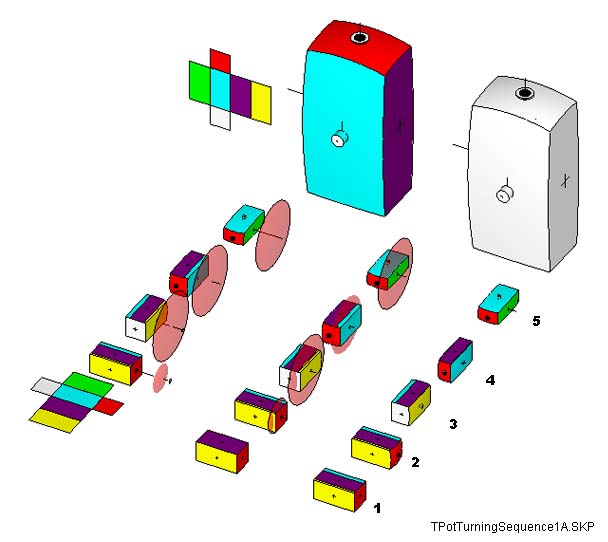
TPotTurningSequence1A.skp (1 Meg download size)
What's different about this Bowl Turner Approach is that, rather than turing the SIDES of a "spindle" held between centers, it's an END that is turned - as if turning the bottom part of a bowl between centers.
The result of this turning sequence is shown, sans the cuts to separate the "pot" from the "lid". While a 2D illustration barely conveys the process or results, you can click on the illustration to download the SketchUp models and explore things in 2 1/2D "virtual models". You can download SketchUp for your operating system for free and install it on your computer.
In THIS model, the face surfaces are CONVEX , but they could be done CONCAVE or a mix of CONCAVE and CONVEX. And while the faces of the sides are centered on the faces of the blank - they DON'T HAVE TO BE CENTERED on the blank faces centers. This "bowl turner" approach can be applied not just to rectangular blanks, but to poygonal blanks as well - and as Barabara says - the possibilities ARE ENDLESS!
If you have suggestions on how to improve this info or questions about this stuff, or just want to comment on it - please e-mail me